Theorem of Three Shapes

of the Elementary Geometry

 

A relationship between the incircles

of three simple geometrical shapes.

 

by

Markus Heisss

2019, Würzburg, Bavaria

 

 

(To copy the following pictures is allowed, but without changes.)

 

 

Given are three shapes, which can take the following forms:

Triangle, regular polygon (including circle and polygram)

and tangential quadrilateral (including kite and dart).

 

Theorem: Transform a given shape 1 into another shape 2 with the same area as shape 1,

and into a further shape 3 with the same perimeter as shape 1,

 but which is similar to shape 2,

then the inradius of shape 2 is the geometric mean

of the inradii of shape 1 and shape 3,

 and so we have the formula:

 

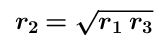
(Discovered in 2016 by Markus Heisss; published as problem in:

“Die Wurzel - Zeitschrift für Mathematik, Heft 11/2016, p. 263”, www.wurzel.org)

 

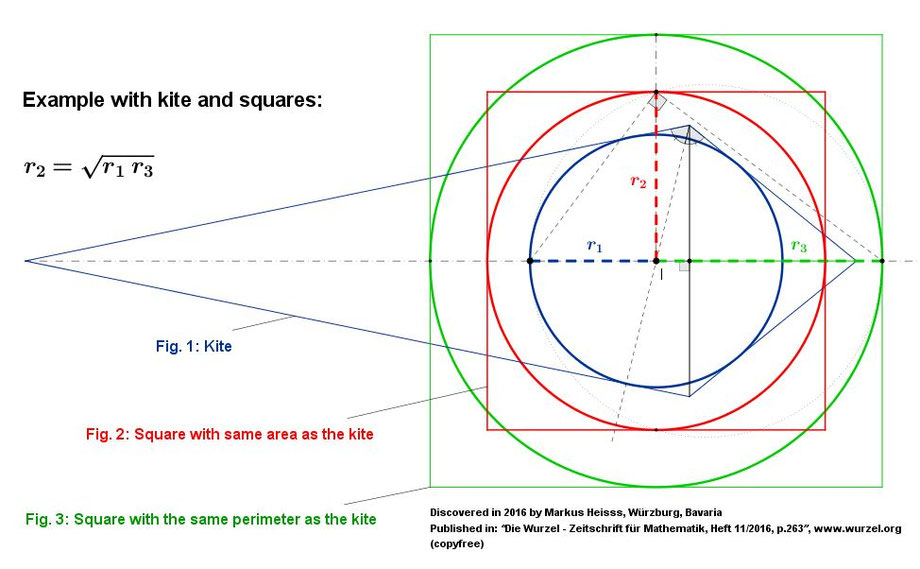
Example 1: Transform a kite into a square with the same area, and into a square with the same perimeter as the kite, then the inradius of the square with die same area is the geometric mean of the inradii of the kite and the square with the same perimeter.

 

Elementary Geometry; Theorem of Three Shapes;

 

 

Example 2: Transform a scalene triangle into an equilateral triangle with the same area, and into an equilateral triangle with the same perimeter as the scalene triangle, then the inradius of the equilateral triangle with die same area is the geometric mean of the inradii of the scalene triangle and the equilateral triangle with the same perimeter.

 

Elementary Geometry; relationship of three shapes; incircles; geometric mean; Heisss

 

 

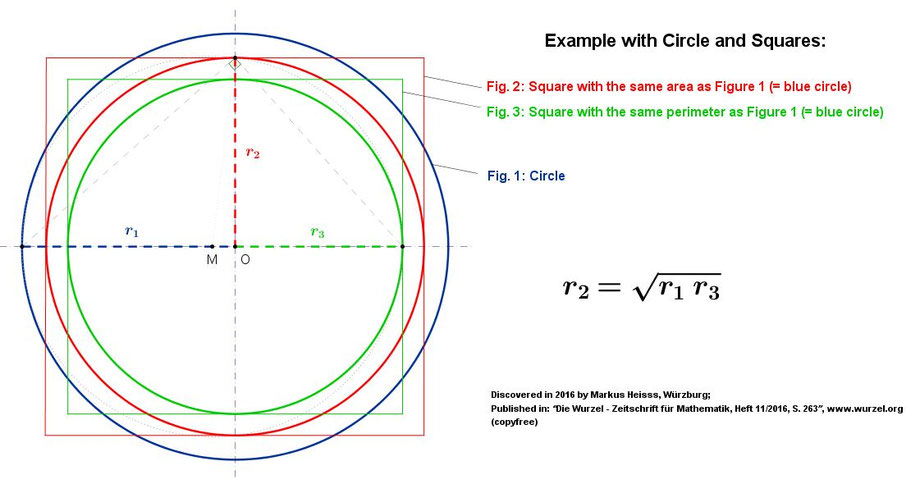
Example 3: Transform a circle into a square with the same area, and into a square with the same perimeter as the circle, then the inradius of the square with die same area is the geometric mean of the inradii of the circle and the square with the same perimeter.

 

That means: Would it be possible to rectify a circle, then the squaring of the circle would be possible, too.

(Rectification, in Geometry, means the finding of a right line equal to a curve.)

 

Elementary Geometry; squaring the circle; Theorem of Three Shapes; discovered and published in 2016 by Markus Heiss (or Heisss)

 

 

Example 4: Transform a dart (or arrowhead, = concave kite) into a square with the same area, and into a square with the same perimeter as the dart, then the inradius of the square with die same area is the geometric mean of the inradii of the dart and the square with the same perimeter.

 

Construction of the incircle of a dart (or arrowhead, or concave kite)
Elementary Geometry; geometric shapes; theorem of three shapes, forms, figures; by Heisss

 

The Proof:

 

Theorem of Three Geometrical Shapes of the Elementary Geometry; the Proof Part 2; by Heisss; the Proof; discoverd and published in 2016 by Markus Heiss (or: Heisss), Würzburg, Bavaria
Theorem of Three Geometrical Shapes of the Elementary Geometry; the Proof Part 2; by Heisss

 

Final remark: As shown, the law is valid for all (regular and irregular) tangential polygons, for which therefore the formula

A = r s  can be used. There are also simple geometric shapes, for which the formula doesn't work, as for example rectangles or semicircles. Here the definition for an incircle is not fulfilled, because not all sides of the polygon get touched by the incircle.

Of special interest are shapes like polygrams (e.g. pentagram) or darts. These don't have a "real" incircle. But if their sides are prolonged beyond the vertices, then it is possible to construct a "pseudo incircle" which fulfills the condition A = s rpseudo

... and consequently the "Theorem of Three Shapes" works!

 

 

References:

Magazine: “Die Wurzel - Zeitschrift für Mathematik, Heft 11/2016, p. 263”, www.wurzel.org

Website: https://markus-heisss.jimdofree.com/geometrie-handskizzen/

 

*****************************

 

Are you interested in my other geometrical discoveries?

[here]